Option Greeks Definitions
옵션 그리스어 정의
BySteve Burns

Options Delta Meaning
옵션 델타 의미
What is delta in options? The delta of an option is part of the option Greek pricing model and prices in the magnitude of the move in the underlier that the option will capture based on the odds of the option expiring in-the-money.
옵션의 델타는 무엇입니까? 옵션의 델타는 옵션 그리스의 가격 책정 모델의 일부이며 옵션이 내가격이 만료되는 확률을 기반으로 옵션이 포착할 기초자산의 움직임 규모에 대한 가격입니다.
Option delta is represented as the velocity of a price change in an option with a 1 point move in the underlying asset and is displayed as a decimal value most of the time. Delta values range between 0 and 1 for call options and -1 to 0 for put options. Delta quantifies the amount an option contract is exposed to moves in the price of the underlying asset. Delta values are set in a range of a positive 1.0 to a negative -1.0, some express a .50 Delta by saying 50.
옵션 델타는 기초 자산에서 1포인트 이동하는 옵션의 가격 변동 속도로 표시되며 대부분의 경우 십진법 값으로 표시됩니다. 델타 값의 범위는 콜 옵션의 경우 0에서 1, 풋 옵션의 경우 -1에서 0입니다. 델타는 옵션 계약이 기초 자산 가격의 움직임에 노출되는 금액을 수량화합니다. 델타 값은 양수 1.0에서 음수 -1.0의 범위로 설정되며 일부는 50을 말하여 .50 Delta를 표현합니다.

그래프 델타와 주식가격
The delta of an option is the sensitivity of an option price to movement in relation to changes in the price of the underlying asset. It tells option traders how much the price of the option will change as the underlying stock or security moves. A deep in-the-money option that is close to expiration will move nearly 100% dollar for dollar with its underlying stock when it has a 1.00 delta. While an at-the-money option will have a delta of .50, and will move 50% in step with its underlying stock or asset.
옵션의 델타는 기초 자산의 가격 변화와 관련하여 옵션 가격의 움직임에 대한 민감도입니다. 그것은 옵션 거래자들에게 기본 주식이나 증권이 이동함에 따라 옵션의 가격이 얼마나 변할지를 알려준다. 만기가 임박한 Deep-in-the money 옵션은 1.00 델타가 있을 때 기본 주식과 함께 달러당 거의 100% 달러를 움직일 것이다.At-the-money 옵션은 .50의 델타를 가지며 기본 주식 또는 자산과 함께 보조를 맞츠어 50 % 이동합니다.
If your stock is at $100 and you have a $100 strike call option and the stock goes up $2.00 your option with a .50 delta will only go up $1.00. As an option gets deeper in-the-money and the odds of it expiring with its intrinsic value increases the delta expands in relation to these probabilities. An at-the-money option has 50/50 odds for directional movement and how it expires in relation to its strike price. As it gets deeper in-the-money the odds grow to 60%, 70%, or 80% of it staying in-the-money as it gets farther from the current price.
귀하의 주식이 $100이고 $100 행사가 콜옵션이 있고 주식이 $2.00 오르면 .50 델타 옵션은 $1.00만 오르게 됩니다. 옵션이 내가격이 깊어지고 내재 가치와 함께 만료될 확률이 높아짐에 따라 이러한 확률과 관련하여 델타가 확장됩니다. 등가격 옵션은 방향 이동에 대해 50/50의 확률을 가지며 행사가와 관련하여 만료되는 방법을 가집니다. 내가격이 깊어질수록 현재 가격에서 멀어질수록 내가격에 머무를 확률이 60%, 70% 또는 80%로 증가합니다.
Calls and puts have opposite deltas, call options are positive and put options are negative. A put option moves inversely to a call option if it is the same distance from current price.
콜과 풋은 반대 델타를 가지며 콜 옵션은 양수이고 풋 옵션은 음수입니다. 풋 옵션은 현재 가격과 동일한 거리에 있는 경우 콜 옵션과 반대로 움직입니다.
Whenever you are long a call option, your delta will always be a positive number between 0 and 1. When the underlying asset increases in price, the value of your call option will also increase by the call options delta value. When the underlier price decreases the value of your call option will also decrease by the amount of the delta.
콜 옵션을 매수할 때마다 델타는 항상 0과 1 사이의 양수입니다. 기초 자산의 가격이 상승하면 콜 옵션의 가치도 콜 옵션 델타 값만큼 증가합니다. 언더라이어 가격이 하락하면 콜 옵션의 가치도 델타 금액만큼 감소합니다.
Put options have negative deltas, which will range between -1 and 0. When the underlier price increases the value of your put option will decrease by the amount of the delta value. When the price of the underlying asset decreases, the value of the put option will increase by the amount of the delta value.
풋 옵션에는 -1과 0 사이의 음수 델타가 있습니다. 기본 가격이 상승하면 풋 옵션의 가치는 델타 값만큼 감소합니다. 기초 자산의 가격이 하락하면 풋옵션의 가치는 델타 가치만큼 증가합니다.
Delta can be a good measure of the current odds of an option expiring in-the-money but those probabilities can change rapidly. An at-the-money option has 50/50 odds of it going either way by expiration and that is reflected in the delta of .50. However if you are buying a far out-of-the-money option with a delta of .10 that moves only one tenth in step with the underlying asset the odds are about 90% that your option will expire worthless. While 1 in 10 are terrible odds and if 9 losses all come in a row as the first nine option trades it could blow up an account if the bets are too big. Option sellers like to write low delta option contracts to sell them short for a high probability of keeping the premium as a profit.
델타는 내가격이 만료되는 옵션의 현재 배당률을 잘 측정할 수 있지만 이러한 확률은 빠르게 변할 수 있습니다. 등가격 옵션은 만기까지 어느 쪽이든 갈 확률이 50/50이며 이는 델타 0.50에 반영됩니다. 그러나 기본 자산과 단계적으로 1/10만 이동하는 델타가 0.10인 외가격 옵션을 구매하는 경우 옵션이 가치없게 만료될 확률은 약 90%입니다. 10분의 1은 끔찍한 확률이고 처음 9개의 옵션 거래에서 9개의 손실이 모두 연속적으로 발생하면 내기가 너무 크면 계정이 폭파될 수 있습니다. 옵션 매도자는 낮은 델타 옵션 계약을 작성하여 프리미엄을 이익으로 유지할 높은 확률을 위해 매도하는 것을 좋아합니다.
Options with .10 Delta can be looked at as lottery tickets with low odds of success. A 1.00 Delta option can be looked at as a replacement for stock but with less capital needed for the position. Delta shows you how much you make on a move and if your strike price is a good bet by expiration.
10 Delta 옵션은 성공 확률이 낮은 복권으로 볼 수 있습니다. 1.00 델타 옵션은 주식의 대체품으로 볼 수 있지만 포지션에 필요한 자본은 적습니다. Delta는 귀하가 이동 중에 얼마나 버는지, 그리고 귀하의 행사가가 만기까지 좋은 베팅인지를 보여줍니다.
By combining different date and strike options in an option play you can create a combined delta for the play through hedges. This will change as prices move and options approach expiration.
옵션 플레이에서 다른 날짜와 행사가 옵션을 결합하여 헤지를 통해 플레이를 위한 결합된 델타를 만들 수 있습니다. 이것은 가격이 움직이고 옵션이 만기에 가까워짐에 따라 변경됩니다.
Options Vega Explained
옵션 Vega 설명
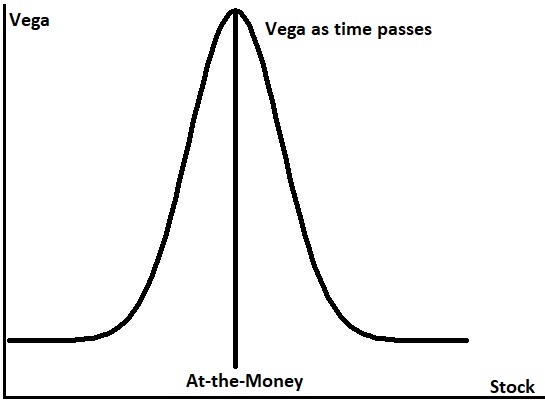
시간이 지남에 따른 베가
Option contract prices will increase as the probabilities of them expiring in-the-money are greater and will go down as the probabilities of them expiring in-the-money decreases. As options get closer to being in-the-money they capture more of their underlying assets move, as they get farther away from being in-the-money they capture less of their underlying assets move. High volatility increases the odds of an option having the ability to be in-the-money on expiration. Extreme volatility also increases the risk of loss to the option seller with a strong adverse move and an option price will increase to account for the higher risk and compensate the option seller for this risk.
옵션 계약의 가격은 내가격이 만료될 확률이 높을수록 오르고 내가격이 만료될 확률이 낮을수록 하락합니다. 옵션이 내가격에 가까워짐에 따라 기본 자산 이동을 더 많이 포착하고 내가격에서 멀어질수록 기본 자산 이동을 덜 포착합니다. 높은 변동성은 옵션이 만기 시 내가격이 될 가능성을 높입니다. 극단적인 변동성은 또한 강한 불리한 움직임으로 옵션 매도자에게 손실 위험을 증가시키며 더 높은 위험을 설명하고 이 위험에 대해 옵션 매도자에게 보상하기 위해 옵션 가격이 상승합니다.
Vega measures an option’s sensitivity when there are changes in volatility of the underlying asset.
Vega는 기초 자산의 변동성 변화가 있을 때 옵션의 민감도를 측정합니다.
Option vega is the measure of the amount of money per underlying share that an option contract value will gain or lose as price volatility rises or drops by 1 percentage point. Both call options and put options will increase in contract value when price volatility rises.
옵션 베가는 가격 변동성이 1% 포인트 상승하거나 하락할 때 옵션 계약 가치가 얻거나 잃을 기초 주당 금액을 측정한 것입니다. 가격 변동성이 커지면 콜옵션과 풋옵션 모두 계약 가치가 높아집니다.
Vega can be one of the most important Greeks to understand and track for an option trader. During more volatile markets and charts the value of option strategies will be very price sensitive to changes in volatility, especially with extreme price range expansion. The cost of at-the-money options, and especially straddle and strangle option plays will become more expensive with changes in volatility on the underliers.
Vega는 옵션 거래자를 위하여 이해하고 추적하는 가장 중요한 그리스언어 중 하나가 될 수 있습니다. 변동성이 더 큰 시장과 차트에서 옵션 전략의 가치는 변동성 변화에 매우 가격에 민감할 것이며, 특히 극단적인 가격 범위 확장과 함께 그렇습니다. 등가격 옵션, 특히 스트래들 및 스트랭글 옵션 플레이의 비용은 언더라이어의 변동성 변화로 인해 더 비싸질 것입니다.
The volatility of an asset is measured by the magnitude and speed that price moves up or down, and can be based on any changes in the recent price range or historical prices in a stock or commodity future contract. Vega will change as there are large price changes in a stock or commodity an option is written on. Vega value in the price of an option will decrease as the option gets close to it’s expiration date or it gets past a risk event like earnings or any other important announcement that could cause a big price move. Vega is the component in pricing of options to account for the risk that a seller is taking on based on the current and estimated volatility of the underlying stock. Options increase in value during times of greater volatility and decrease in times of less volatility and after risk events have passed.
자산의 변동성은 가격이 위아래로 움직이는 크기와 속도에 의해 측정되며 최근 가격 범위 또는 주식 또는 상품 선물 계약의 역사적 가격 변동을 기반으로 할 수 있습니다. Vega는 옵션이 작성된 주식이나 상품에 큰 가격 변동이 있을 때 변경됩니다. 옵션 가격의 Vega 가치는 옵션이 만기일에 가까워지거나 수익과 같은 위험 이벤트 또는 큰 가격 변동을 일으킬 수 있는 기타 중요한 발표가 지나면 감소합니다. Vega는 기본 주식의 현재 및 예상 변동성을 기반으로 매도자가 감수하는 위험을 설명하기 위한 옵션 가격 책정의 구성 요소입니다. 옵션은 변동성이 큰 시기에는 가치가 상승하고 변동성이 적은 시기에는 위험 이벤트가 지나간 후에 가치가 하락합니다.
If you purchase a stock that is on a company that will announce its earnings before the options expire the expected volatility and the move of the price that is expected due to that event will be priced into the option. An at-the-money option will give you an idea of the expected move of a stock. If a stock is at $100 and an at-the-money $100 strike call option is normally $3 one week until expiration but earnings are before expiration and the $100 strike is $13 instead of the normal $3 then the odds are that the $3 is the normal theta value and the extra $10 is the vega value pricing in a $10 move after earnings. One thing that trips up new option traders is that that $10 Vega value will be almost completely gone when the option opens for trading the following morning after earnings are announced and digested on the chart.
The stock could open at $110 and your option still be worth $13 as your Vega value has been replaced by intrinsic value and you could still have $3 in theta value. To trade options through earnings you have to overcome the price of the volatility that will be gone after the event with enough intrinsic value of the option going in-the-money to be profitable. Some vega can also be priced into options before major events like Fed minutes, a congressional bill, a crop report, or a big jobs report. Always be aware that options are pricing in moves in time and volatility to compensate the option sellers for their risk taking. Option pricing is very efficient for the known volatility of events. It is the following of trends, systems, reactive technical analysis, and risk/reward ratios that can provide an edge.
Vega tends to expand and retract over time. Markets go from volatile to trending or range bound and back to volatile over time and vega tracks the risk in volatility by pricing it into options contracts. Peak vega pricing is with the at-the-money option in a chain and decreases as options get farther in-the-money or farther out-of-the-money as the probabilities change for the option expiring in the money due to volatility.
Options Theta Definition
Gxti / CC BY (https://creativecommons.org/licenses/by/3.0)
Theta is also called time decay in the option world as the value of an option declines day after day. Theta measures the time value that you pay to hold the contract, in essence you are paying to rent the shares for a set period of time. This is in addition to any intrinsic value of the option if it is in-the-money. A percentage of your time value disappears out of the price of the option each day that you hold the contract after it is purchased. Options are wasting assets, their life span is set only until the expiration date and at that time the option owner has the right to call the stock to be bought at the strike price for a call option or to put a stock on someone for the strike price of a put option. The Theta value is like the countdown clock where time is money on the path to the expiration giving the option buyer the right to execute the contract.
At expiration the time value is zero and you are left with the difference in the intrinsic value that the option entitles you to buy or sell a stock for versus the open market price. The velocity of the time value decline starts out slower when the option is months away from expiration and accelerates in the final month to expiration and is very fast in the last week before expiration.
Far out-of-the-money options and far out-of-the-month options are made up almost entirely of time value along with volatility as they try to price in if any events will happen before expiration to cause them to end up in-the-money. Options so far away in time and price do not have any other type of value but time.
On the last day of an options expiration the option will have almost zero time value as only one day is left. Just remember that when you enter a stock option trade you are on the clock. The stock has to move close enough to the price of your stock to pay for the time you spend holding it. For a longer term trade you have to overcome the cost of time to be profitable in your option.
Stocks have no time expense, you are not renting a stock when you own it you are taking on the full risk of the asset. With options you have to pay rent to own the rights to buy or sale a stock at a certain price over a time frame. The Theta value is what you are paying someone for the time they spend exposed to the risk of you calling or putting an asset on them at expiration.
Options Gamma Explained
JWillette, CC BY-SA 3.0 <https://creativecommons.org/licenses/by-sa/3.0>, via Wikimedia Commons
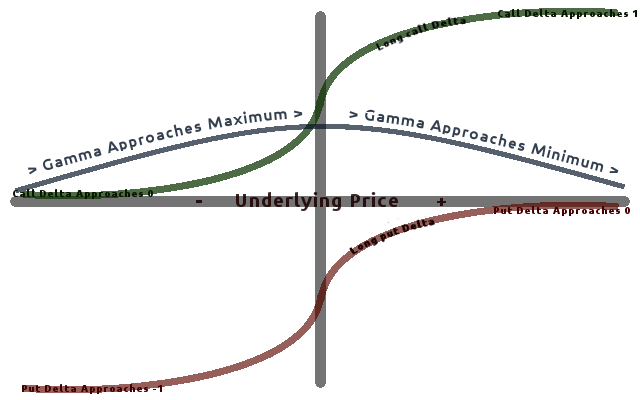
Gamma is the measurement of the rate of change of the delta.
Gamma is the Greek that shows how delta will change with the underlier’s price moves. It is the rate of change of an option’s delta based on a $1.00 move in price of the underlier.
Gamma describes how much the options delta changes as the price of the underlying stock changes. The option’s gamma value is a measurement of the speed of change of the option’s delta. The gamma value of an option contract is a percentage and shows the change in the delta when there is a one point move in the price of the underlying stock. The options gamma value measures the magnitude and the direction of a change in the option’s delta.
When a long call option contract has a gamma of 0.10 and a corresponding delta of 0.50, When the underlier goes up $1.00 in price, that specific option will have an option Greek delta of 0.60 as one dynamic of its price movement in correlation with the underlier. It is important to understand the gamma of a stock as it can show the risk and benefits of the rate of change as an option moves closer or farther from being in or out-of-the-money. Short option risks is one of the most important dynamics to consider with gamma as the option price can move strongly against you quickly during a trend or gap in price with the underlier.
Deltas expand and become higher as price moves in favor of your option’s strike price. Options capture more intrinsic value as price moves closer to being in-the-money versus your options strike price. Deltas become smaller as price moves away from your option positions strike price needed for the option to go in-the-money. As price moves away from your strike price needed for profitability the movement becomes smaller on the option as the delta declines the gamma also declines.
A Gamma scalper of options is simply trying to buy an out-of-the-money option with nothing but time value and a very low delta and profit by the option delta expanding and increasing in value. An out-of- the-money option with very little premium value can go up in price as the odds of it going in-the-money increases and the delta capture rapidly expands.
A Gamma scalper will buy an option with only Theta value and profit from the gamma of a rapidly increasing delta. These types of trades usually have lower win percentages but can be profitable with wins that are 100% or more of price value. The key with these types of trades which many new option traders love is to trade them with a small amount of trading capital. 0.25% or 0.5% of total trading capital at risk is a good position size for these types of high reward but low probability of success trades. A gamma scalper does not need his option to go in-the-money to be profitable, he only needs the odds of it going into the money to increase so he can sell it for a profit.
Benefits of Gamma
Gamma can be most profitable for long option trades as it can grow profits fast when an out-of-the-money option gets close to being in-the-money. This can cause triple digit gains in option price on the long side. Losses also get smaller as an option moves farther away from being in-the-money to create a favorable risk/reward ratio. Gamma will increase until an option goes deep-in-the-money with a delta at 1.00. The ideal long option gamma trade is a far-out-of-the-money option becoming a deep-in-the-money option that maximizes gains.
Short Options Gamma Risk
Gamma presents the single biggest risk to option sellers as the attempt to write options for the small gain from theta can lead to big losses from gamma, especially for short unhedged option plays.
Options Expiration and Gamma
The risk to long option gamma traders is limited to the price of the option contract while the upside profit potential is theoretically unlimited. The maximum risk on the long side is that the option contract becomes worthless on expiration. The maximum risk for an option trader writing contracts short is theoretically unlimited with no hedge and the primary risk is the gamma growing exponentially.
The gamma curve plunges as expiration approaches as the odds of expiring in-the-money drops to lower probabilities. As the odds of delta expansion declines gamma declines along with it. Gamma expansion is great for option buyers but can cause option sellers large losses. Gamma growth can turn a losing long option trade into a winner quickly and also turn a winning short option trade into a loser just as quick.
Options Rho Explained
Rho measures the sensitivity of a stock option price to a change in interest rates. Rho measures and prices in to an option contract the expected change in price for every one percentage point change in current interest rates. It shows option traders how much the price of an option contract should go up or down if the risk free interest rate like on U.S. Treasury-bills rises or falls.
Rho is almost never considered in today’s options market due to the stability of interest rates the vast majority of the time over the last decade. Interest rates use to be a consideration in pricing before recent times when rates have gone flat basically or to zero. Recent increases in rates could make rho a factor again.
I created my Options 101 eCourse to give a new option traders a shortcut to a quick and easy way to learn how stock options work.

'거래기술에 관한 정보' 카테고리의 다른 글
| Price Action vs Indicators (0) | 2022.06.25 |
|---|---|
| Common Mistakes in Technical Analysis (0) | 2022.06.23 |
| Trend Following Trading Strategy Guide(추세 추종 거래 전략 가이드) (0) | 2022.06.10 |
| Option Strategies For High Volatility(고변동성을 위한 옵션 전략) (0) | 2022.06.07 |
| What is a Parabolic Curve in Stocks? (0) | 2022.06.06 |