What Is A Monte Carlo Simulation?(몬테카를로 시뮬레이션이란?)

 

What Is A Monte Carlo Simulation?(몬테카를로 시뮬레이션이란?)

Posted By: Steve Burnson:

Enter your email address and we'll send you a free PDF of this post.

Share this:

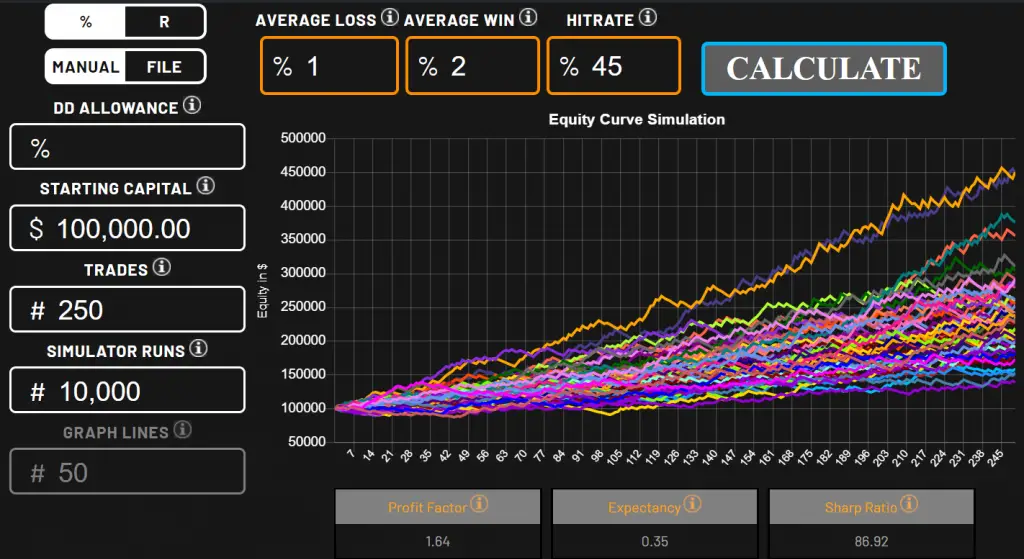
A Monte Carlo simulation is a process used to show all the potential outcomes of a trading system, business model, supply chain, scientific theory, insurance, research and development, or a casino. A Monte Carlo simulation uses the most important available metrics of a system including inputs of size of wins and losses along with win rates and other probabilities to compute all the future possibilities of a system or process. 

Monte Carlo 시뮬레이션은 거래 시스템, 비즈니스 모델, 공급망, 과학 이론, 보험, 연구 개발 또는 카지노의 모든 잠재적 결과를 보여주기 위해 사용되는 프로세스입니다. Monte Carlo 시뮬레이션은 시스템 및 프로세스의 모든 미래 가능성을 계산하기 위해 승률 및 기타 확률과 함께 승 수 및 손실 크기의 입력을 포함하여 시스템의 가장 중요한 가용 메트릭을 사용합니다.

A Monte Carlo simulation does multiple (수행하다)risk and reward calculations by creating potential models of multiple outcomes by processing a wide range of values to create a graphic of probability distribution. It attempts to remove some of the uncertainty of implementing a system by showing the range of potential outcomes based on the factors of the system. It can calculate new results after the parameters of a system are adjusted to look for better potential outcomes. A Monte Carlo simulation can show thousands of potential outcomes based on the input of variables in a system. 

Monte Carlo 시뮬레이션은 광범위한 값을 처리하여 확률 분포 그래픽을 작성하여 여러 결과의 잠재적 모델을 작성하여 여러 위험 및 보상 계산을 수행합니다. 시스템의 요소를 기반으로 잠재적 결과 범위를 보여줌으로써 시스템 구현의 불확실성을 제거하려고 시도합니다. 더 나은 잠재적 결과를 찾도록 시스템의 매개 변수를 조정 한 후 새로운 결과를 계산할 수 있습니다. Monte Carlo 시뮬레이션은 시스템의 변수 입력을 기반으로 수천 개의 잠재적 결과를 보여줄 수 있습니다

The purpose of a Monte Carlo simulation is to create and show the variance of distribution of possible outcome results based on the parameters of a system. It is used for risk management and optimization of rewards for a system with measurable inputs. It seeks to create some clarity around future results.  

Monte Carlo 시뮬레이션의 목적은 시스템의 매개 변수를 기반으로 가능한 결과 결과 분포의 분산을 작성하고 표시하는 것입니다. 측정 가능한 입력이있는 시스템의 위험 관리 및 보상 최적화에 사용됩니다. 미래의 결과에 대한 명확한 설명을 모색합니다.

 

몬테카를로 시뮬레이션 (Monte-Carlo Simulation)

http://yjhyjh.egloos.com/33072

연구(R&D) 기획일을 하다보면 불확정적인 정보들로 인해 결론내리기가 애매한 경우를 많이 당한다.
특히, 나를 포함한 공학도 출신들은 정확히 딱딱 떨어지는 계산결과에 쾌감마져 느끼는 사람들이 많다. 이런 사람들은 '이럴수도 있고, 저럴수도 있다'라는 식의 정보가 나오게 되면 결과를 내놓고도 결과가 흔들릴 수 있다는 생각에 잠이 잘 안오곤 한다.
기획은 planning이기 때문에 forecasting과 추론을 포함할 수 밖에 없다. 그리고 여기에 영향을 미치는 대부분의 요소들은 확률변수이다.
확률이 존재하는 의사결정이 필요한 상황에 내가 종종 들고 나오는 무기(tool)는 몬테카를로 시뮬레이션(Monte-Carlo Simulation)이다.

<몬테카를로 시뮬레이션의 개요>
변수의 관계가 확실하여 예측치를 정확하게 찾을 수 있는 확정모형(deterministic model)과는 달리, 기획일의 많은 부분은 결과를 정확하게 예측할 수 없는 확률모형(stochastic model)이다. 일반적으로 확정모형에서는 분석적 해(analytical solution)을 찾는 것이 가능하다. 그러나 확률모형에서는 분석적인 방법으로 해를 찾는 것이 불가능 한 경우가 많다. 이 경우에는 수치적(numerical)으로 일련의 난수를 반복적으로 발생해서 시뮬레이션을 하면 답을 찾을 수 있는데 이것이 몬테카를로 시뮬레이션이다.

기본 사상은 각각의 단위 변수의 패턴을 알아내서, 의사결정을 위한 그 단위 변수의 조합의 패턴을 추정하는 것이다.
다시말해, 각각의 변수의 확률분포를 통합해서 목표로 하는 값의 확률분포를 알아내는 것이다.
Figure 1.을 보면 이게 무슨말인지 쉽게 이해할 것이다.

< Figure 1 >

그럼 단위 변수들의 확률모델은 어떻게 알아내느냐고? 그건 최소한 의사결정을 위한 목표값의 확룔모델을 알아내는 것보다는 몇갑절 쉽고 정확하다. 범위와 그 속성을 알면 누구나 동감할 만한 수준의 패턴을 찾아낼 수 있기 때문이다.

몬테카를로 시뮬레이션에 대한 비교적 이해하기 쉬운 글이 하나 있어서 추천한다. 아래를 클릭해서 읽어보면 도움이 될 것이다.
http://www.nemopartners.com/webzine/webzine0504_10.asp

이즈음에서 실제 적용사례를 하나 예로 들어보자.
일단, 몬테카를로 시뮬레이션을 돌릴 툴이 필요하다. 각종 나이스한 통계툴들이 많이 판매되고 있지만, 이거 하겠다고 SW사달라고하면 사줄회사가 몇이나 될까? 대기업인 우리도 절대 사줄리 없다. 나중에 그 효용이 공유되고 아주 많은 경우에 통계기법이 활용되는 상황이 펼처지면 그때는 사줄 것이다. 그러므로 많은 분들은 엑셀을 써야만 하는 환경에 있으리라 믿어 의심치 않는다. (여기에 내가 그렇게 노래를 부르는 MS Excel의 power user가 되어야 하는 이유가 있다.)
엑셀을 이용하여 몬테카를로 시뮬레이션을 돌리는 것과 관련해서는 경문사의 '(엑셀/VBA를 이용한) 금융공학' 책을 읽어볼 것을 추천한다. 어느정도 수준급의 사용자는 굳이 이책을 읽지않고도 스스로 엑셀을 이용한 분석툴을 디자인 할 수 있겠지만 말이다.
이 예제에서는 모두 3가지 변수를 사용하여, 목표지수를 알아내려는 시도를 한다.
3개의 변수(A, B, C)는 향후 몇년간 주어진 범위 내에서만 움직일 것이 확실하지만, 정확히 어떤값이 될지는 기업내외부 사정에 따라서 달라지므로 무어라 탁 꼬집어 말할 수 없는 상황이다. 다행히 A와 B의 트랜드는 파악이 되어서 어느정도 패턴을 유추할 수는 있는 상황이다. Metric C는 패턴이란게 절대 안보이고 범위안에서 제멋대로 나오므로 random변수를 사용할 수 밖에 없다.
3개의 변수에 대한 범위와 그 패턴정의는 Figure 2.와 같다.

< Figure 2 >

Metric	Variation	Distribution
A	0~2	normal
B	0.6~0.8	exponential
C	0.10~0.15	uniform

이러한 조건을 이용해서, 각 Metric의 난수생성을 해보자. (엑셀의 함수기능을 활용해야 하는데, 그것은 위에 추천한 책이나 엑셀의 도움말을 보고 공부하도록 한다. 여기서 엑셀 강좌까지 할 수는 없지 않은가?)
임의로 각각 2천개씩 생성해서 돌리면 어느정도 답의 패턴이 보인다. 금융공학에서는 1백만번 이상이 되면 신뢰할만하다고 말을 하는데, 프로그래밍 하지않고 엑셀의 기능만 이용하면 이건 현실적으로 불가능하고 꼭 그렇게 안해도 2천번이면 충분히 결과가 나오더라.
Figure 3.은 2천개의 난수패턴에 결합모델을 이용한 엑셀파일의 일부이다. 오만가지 경우에 대한 목표지수가 나열된다. 몇개가? 2천번 돌렸으니 2천개가!

< Figure 3 >

Figure 3.을 보면 일단 무슨짓을 한것인지는 알 수 있을 것이다. 각 경우에 대한 목표값을 일일이 만들어보는 것이다. 사람이 할 짓이 아니므로, 컴퓨터가 필요한 것이 바로 몬테카를로 시뮬레이션이다.

Figure 4.은 각 Metric과 목표지수의 결과값을 오름차순으로 sorting해서 그 패턴을 분석해본 것이다. 과연, 확률모델상에서는 어떤일이 벌어진건지 설명해주기 위해서, 별도로 만들어 본 것이다. (목표지수도 sorting된 것이므로 Figure 3.에서처럼 Metric A, B, C의 연산으로 산정되는 테이블이 아님을 명심할 것)

< Figure 4 >

위의 Figure 4.를 보면 A와 B와 C의 패턴이 만나서, 목표값의 패턴이 되는 과정을 볼 수 있다. (사실 막대그래프인데 2천개를 정렬해서 세워놓으면 이런 차트가 나온다. 미적분의 원리 아닌가? ^^)
물론 목표값자체도 확률모델로 나오므로, 1개의 정확한 해가 구해지는 것은 아니다. 하지만 적어도 의사결정에 사용될 결과값이 어떻게 움직일지가 예상될 수 있드며, 목표값이 어느 부분에 집중되어 있으므로 어디를 공략하는게 성공율이 높은지의 정보가 나온다.
충분히 값진 결과이다.


<몬테카를로 시뮬레이션 결과의 보고>
몬테카를로 시뮬레이션 결과는 어떻게 보고 되어야 할까?
난 편의상 복잡한 것을 싫어하는 상사에게는 가장 빈도높고 성공확률 높은 값(통상적으로 평균이 되는 경향이 있지만)을 찾아내서 그것을 알려주기도 한다. 하지만, 이것은 상황에 따라 그러는 것이고, 정공법은 아니다.
몬테카를로 시뮬레이션의 결과는 확률로 보고되는것이 정공법이다.
결과값은 각 구간별 빈도수를 체크하여 차트로 구성한다. 그러면 각 구간별로 발생할 수 있는 확률패턴이 나타나게 되는데 이것이 의사결정에 도움이 된다. (가장 대표적인게 표준정규분포표 아닌가?)

Figure 5.는 톰 디마르코와 티모시 리스터의 '소프트웨어 프로젝트에서의 리스크 관리'란 책에서 제공하는 Riskology라는 엑셀로 개발된 툴을 이용한 결과이다. (힌트를 주자면, 위에서 언급한 예제를 빈도수를 가지고 히스토그램을 만들어보면 아래와 똑같은 모양이 된다. 한번 해보기 바란다.)

< Figure 5 >

이것은 특정 프로젝트의 완료일자에 영향을 주는 다양한 요소를 고려해서 만들어진 완료일자 확률모델이다.
프로젝트는 상황이 충분히 좋으면 8월 11일에 종료될 수도 있고, 상황이 어려워지면 이듬해 12월까지 질질 끌려 지연될 수도 있다.
여러분이 이 프로젝트를 맡았다면, 언제까지 과제를 종료시키겠다고 말할 것인가? 영업에선 8월 중에 종료할 수있다고(사실은 그럴 가능성이 있기는 하지만) 밀어붙이겠지만, 함부로 8월에 끝낼 수 있다고 장담할 수 있는 사람은 없을 것이다.
그러면, 어떻게 보고를 해야 할까? 내년 5월 완료? 7월 완료? 이쯤되면 그만두란 소리를 들을 법도 하다.
몬테카를로 시뮬레이션을 이해하는 사람간의 대화라면 아마 다음과 같을 것이다.
"이 프로젝트를 금년 10월까지 성공적으로 완료할 수 있는 확률은 15%남짓 합니다. 하지만 올해 12월까지 완료될 가능성은 30%는 되므로, 출시일정을 이에 맞추면 30%이상의 성공을 기대할 수 있을 것 같습니다."
이 대화가 이상해 보이는가?
난 이정도로 정량화된 사고와 대응을 할 수 있는 후배라면, 돈이 얼마나 들던 꼭 데려오고 싶을 것 같다.

참고로, Figure 5와 같은 모델을 리스크 다이어그램(Risk Diagram)이라고 한다.
이것은 정량적 위험관리의 강력한 툴로 사용된다.
몬테카를로 시뮬레이션이 적극적으로 활용되는 분야가 위험관리인데 이에 대해서는 위험관리에 대한 고찰 (Advanced Risk Management) 포스트를 참조하기 바란다.


<TIP>
몬테카를로 시뮬레이션은 무척 다양한 용도로 쓰인다.
(정량적 위험관리, 사업리스크 분석, 금융공학, 품질관리 등등)
확률이 존재하는 의사결정이 필요한 모든 부분에서 우선적으로 사용을 검토해보길 권한다.
최소한, 기존의 주먹구구 방식보다는 진일보시켰다는 평가를 받을 수 있을 것이다.