Simple interest is only calculated on the original amount of capital inside a set time period. It does not include the compounding effect of returns on new money accrued(발생하다). Simple interest can be used over any time period but annual returns is the one that is most commonly used. Simple interest is calculated on original principle alone. Compound interest includes the additional gains on capital in previous periods. Simple interest is on principle while compound interest can be said to be “interest on interest.
”단순 이자는 정해진 기간 내에 자본의 원래 금액에 대해서만 계산된다. 그것은 발생한 새 화폐에 대한 수익의 복합적인 효과는 포함하지 않는다. 간단한 이자는 어느 기간에도 사용할 수 있지만 연간 수익률은 가장 많이 사용되는 것이다. 단순 이자는 원리에 의해서만 계산된다. 복합이자에는 이전 기간의 자본에 대한 추가적인 이득이 포함된다. 단순 이자는 원칙이고 복리 이자는 "이자에 대한 이자"라고 말할 수 있다.
Here is the formula for compounding simple interest.
단순이익을 복합하는 공식이 여기에 있다.
A = final amount(최종금액)
P = initial principal balance(최초 원금 잔액)
r = interest rate(이자율)
n = number of times interest applied per time period(기간당 적용되는 이자 수)
t = number of time periods elapsed(경과된 기간 수)
Here is an example of 12% simple interest on capital for one year:
1년 동안 자본에 대한 12%의 단순 이자의 예는 다음과 같다.
$112,000 = $100,000 X 0.12% = $12,000 + $100,000
Here is an example of compound interest at 12% over a one year period compounded monthly at 1% resulting in a +12.63% annualized return, this contrasts to simple interest as the returns on new capital creates the compounding of returns.
다음은 1 %로 월 1 % 씩 복리하여 연간 수익률이 12.63 % 인 1 년 동안 복리 이자율이 12 % 인 예입니다. 이는 새로운 자본에 대한 수익률이 수익의 복리를 생성하기 때문에 단순한이자와 대조됩니다.
| Monthly | Compounding |
| 1% | |
| $100,000 | $101,000 |
| $101,000 | $102,010 |
| $102,010 | $103,030 |
| $103,030 | $104,060 |
| $104,060 | $105,101 |
| $105,101 | $106,152 |
| $106,152 | $107,214 |
| $107,214 | $108,286 |
| $108,286 | $109,369 |
| $109,369 | $110,462 |
| $110,462 | $111,567 |
| $111,567 | $112,683 |
The compounding of capital can be a very powerful tool for capital growth while simple interest sets the time frame of returns.
자본의 복합화는 자본증식의 매우 강력한 도구가 될 수 있는 반면 단순한 이자는 수익의 기간을 정한다.
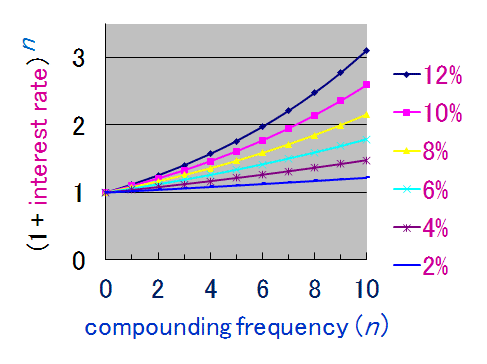
Kazov [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)]